BLOQUE 3

MEDIDAS DE TENDENCIA CENTRAL PARA DATOS SIMPLES Y AGRUPADOS 

Las medidas de tendencia central de datos agrupados se utilizan en estadística para describir ciertos comportamientos de un grupo de datos suministrados, como por ejemplo a qué valor están cercanos, cuál es el promedio de los datos recogidos, entre otros.

MEDIA 

La media es la suma de los valores de todas las observaciones, dividida entre el número de observaciones realizadas.

Sea n el tamaño de una muestra que contiene a las observaciones x1, x2, x3,. . ., xn, entonces la media aritmética, x es:

En donde el subíndice i, indica un número de conteo para identificar cada observación.

Ejemplo:

Encuentre los medios del conjunto {2, 5, 5, 6, 8, 8, 9, 11}.

Hay 8 números en el conjunto. Súmelos, y luego divida entre 8.

= 6.75

Así, la media es 6.75.

MEDIANA 

La mediana es el valor central que se localiza en una serie ordenada de datos. La mediana de una variable X corresponde con el valor central de un conjunto de n observaciones de la variable X ordenadas según su magnitud.

Ejemplo 1 :

Encuentre la mediana del conjunto {2, 5, 8, 11, 16, 21, 30}.

Hay 7 números en el conjunto, y estos están acomodados en orden ascendente. El número medio (el cuarto en la lista) es 11. Así, la mediana es 11.

MODA

La moda es el dato que más se repite o el dato que ocurre con mayor frecuencia.

La siguiente serie de datos tiene dos modas, ya que el 11 y el 15, se repiten 2 veces, entonces se dice que la distribución de los datos es bimodal. 4 6 9 11 11 12 13 15 15

La siguiente serie de datos es trimodal, ya que el 4, el 11 y el 15 se repiten 3 veces. 4 4 4 6 9 11 11 11 12 13 15 15 15

Ejemplo 1:

Encuentra la moda del conjunto {2, 3, 5, 5, 7, 9, 9, 9, 10, 12}.

El 2, 3, 7, 10 y 12 aparecen una vez cada uno.

El 5 aparece dos veces y el 9 aparece tres veces.

Así, el 9 es la moda.

 SESGO 

En estadística se llama sesgo de un estimador a la diferencia entre su esperanza matemática y el valor del parámetro que estima. Un estimador cuyo sesgo es nulo se llama insesgado o centrado.

En notación matemática, dada una muestra   y un estimador   del parámetro muestral θ, el sesgo 

MEDIDAS DE DISPERSIÓN PARA DATOS SIMPLES Y AGRUPADOS 

Las medidas de dispersión son parámetros estadísticos que indican como se alejan los datos respecto de la media aritmética. Sirven como indicador de la variabilidad de los datos. Las medidas de dispersión más utilizadas son:  

·         Rango

·         Desviación media

·         Desviación estándar

·         Varianza

Rango

Indica la dispersión entre los valores extremos de una variable. se calcula como la diferencia entre el mayor y el menor valor de la variable. (R)

Para datos ordenados se calcula como:

R = x(n) - x (1)

Donde: x(n): Es el mayor valor de la variable. x(1): Es el menor valor de la variable.

Desviación media

Es la media aritmética de los valores absolutos de las diferencias de cada dato respecto a

la media.

Donde:

DM: Desviación media

Σ: Sumatoria

||: Valor absoluto (+)

X: Marca de clase

X: Promedio

n: Total de datos 

f: Frecuencia

 

Desviación estándar

La desviación estándar mide el grado de dispersión de los datos con respecto a la media, se denota como s para una muestra o como σ para la población. Se define como la raíz cuadrada de la varianza según la expresión:

Como se puede observar el denominador es n - 1, a diferencia de la desviación media donde se divide entre n; también existe la fórmula de desviación típica donde el denominador es n pero se prefiere n-1.

Mientras menor sea la desviación estándar, los datos son más homogéneos, es decir existe menor dispersión, el incremento de los valores de la desviación estándar indica una mayor variabilidad de los datos.

Varianza

Es otro parámetro utilizado para medir la dispersión de los valores de una variable respecto a la media. Corresponde a la media aritmética de los cuadrados de las desviaciones respecto a la media. Su expresión matemática es: 

donde Xi es el dato i-ésimo y es la media de los N datos.

Coeficiente de Variación

Permite determinar la razón existente entre la desviación estándar (s) y la media. Se denota como CV. El coeficiente de variación permite decidir con mayor claridad sobre la dispersión de los datos.

También puede ser expresado en por ciento.

El siguiente video muestra un ejercicio en el cual  da paso a paso cada parte de las medidas de dispersión. 

Autores: 

Mario Orlando Suárez Ibujes

Medwave

Fuentes:

https://www.ub.edu/stat/GrupsInnovacion/Statmedia/demo/Temas/Capitulo7/B0C7m1t5.htm

https://www.portaleducativo.net/octavo-basico/792/media-moda-y-mediana-para-datos-agrupados

https://www.varsitytutors.com/hotmath/hotmath_help/spanish/topics/mean-median-mode

https://www.medwave.cl/link.cgi/Medwave/Series/MBE04/4934?ver=sindiseno

https://www.ecured.cu/Medidas_de_dispersión

LIMITES ESTADÍSTICOS 

CUARTILES:

Los cuartiles son los tres valores de la variable que dividen a un conjunto de datos ordenado sen cuatro partes iguales.

1. Q₁, Q₂ y Q₃ determinan los valores correspondientes al 25%, al 50% y al 75% de los datos.
2. Q₂ coincide con la mediana.

Cálculo de los cuartiles

1: Ordenamos los datos de menor a mayor. 

2: Mediante las formulas:

         DATOS PAR:                         DATOS IMPAR: 

          QK= kn/4                            QK=(n+1)/4  

Q: Cuartil

K: Número de cuartil

n: número de datos

Número impar de datos

2, 5, 3, 6, 7, 4, 9

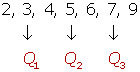
Número par de datos

2, 5, 3, 4, 6, 7, 1, 9

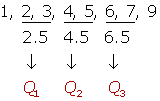
DECILES:

Los deciles son los nueve valores que dividen una serie de datos ordenados en diez partes iguales.

Los deciles dan los valores correspondientes al 10%, al 20%... y al 90% de los datos.

El decil 5 coincide con la mediana: D₅ = Me

El decil 5 coincide con el cuartil 2: D₅ = Q₂ = Me

Cálculo de los deciles

En primer lugar buscamos la clase donde se encuentra ,  
 en la tabla de las frecuencias acumuladas.

L_i es el límite inferior de la clase donde se encuentra el decil.

N es la suma de las frecuencias absolutas.

F_i-1 es la frecuencia acumulada anterior a la clase el decil.

PERCENTILES 

El percentil es una medida de posición no central. Los percentiles P_i son los 99 puntos que dividen una serie de datos ordenada en 100 partes iguales, es decir, que contienen el mismo número de elementos cada una.

Sea (X₁, X₂,…,X_N) una muestra de N elementos. El percentil P_i se calcula mediante la fórmula siguiente:

Donde P_i es la posición del percentil buscado en la serie ordenada de datos.

(N+1)·i/100 pueden resultar números decimales.

 Por ejemplo, si el conjunto de datos es de 200 elementos, N=200, tendremos que el sujeto del percentil 50 será (N+1)·i/100=201·50/100=100,5. 

¿Qué hacemos en el caso de que nos de un número decimal?

Diferenciaremos dos casos:

• Sin parte decimal: elegimos ese mismo sujeto. Por ejemplo, si el conjunto tiene 199 elementos, (N+1)·i/100=200·50/100=100, por lo que el percentil 50 será P₅₀=X₁₀₀.
• Con parte decimal: supongamos que el elemento es un número con parte decimal entre el sujeto t y el t+1. Sea un número de la forma t,d donde t es la parte entera y d la decimal. El percentil será:

Los percentiles están pensados para conjuntos de elementos de más de cien elementos.

Una aplicación muy conocida de los percentiles son las tablas de crecimiento de los niños, en las que se ubica el peso y la talla de un determinado niño dentro de su grupo de edad.

Características de los percentiles

• El percentil 25 (P₂₅) es el cuartil 1 (Q₁).
• El percentil 50 (P₅₀) es la mediana y el cuartil 2 (Q₂).
• El percentil 75 (P₇₅) es el cuartil 3 (Q₃).

El siguiente vídeo muestra un ejemplo acerca de cada uno de los límites estadísticos: 

URL:

CUARTILES:

DECILES: https://www.vitutor.com/estadistica/descriptiva/a_12.html

PERCENTILES: https://www.universoformulas.com/estadistica/descriptiva/percentiles/